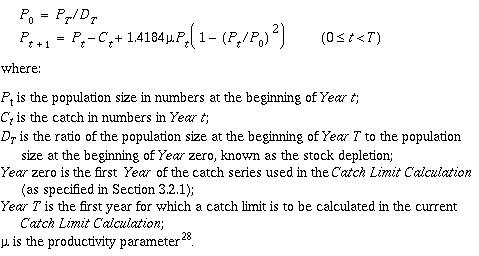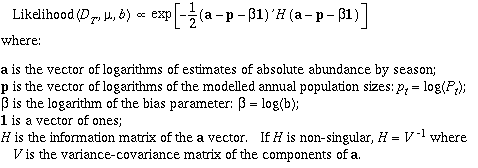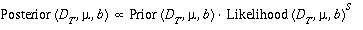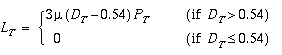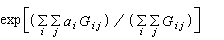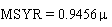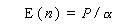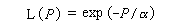(Superscript numbers refer to the appended annotations)

Note:

1. Because of poor support to mathematical symbols by HTML, some formulas are shown as graphic images.
2. Because of poor support to special symbols by HTML, Greek letters in the text are substituted by quoted words like 'alpha', 'mu', etc.)

Regions are non-overlapping major ocean areas. For species found in or migrating to higher latitudes, these will normally be the Arctic and adjacent waters, the North Atlantic and adjacent waters, the North Pacific and adjacent waters, and the Southern Hemisphere. For species confined to lower latitudes, the Regions will normally be the Atlantic, Pacific and Indian Oceans. Regions can be combined for species where the interchange is not negligible.

Small Areas are disjoint areas small enough to contain whales from only one biological stock, or be such that if whales from different biological stocks are present in the Small Area, catching operations would not be able to harvest them in proportions substantially² different to their proportions in the Small Area.

Medium Areas³ correspond to known or suspected ranges of distinct biological stocks.

Large Areas⁴ coincide with Regions, unless evidence exists to support the selection of one or more areas smaller than a Region which fully covers the range of some biological stocks of a species and definitely excludes whales from all other biological stocks of that species in the Region.

Residual Areas⁵ are all geographical areas in a Region which are outside any Small Areas. Medium Areas comprise unions of Small and, where identified, Residual Areas. Large Areas comprise unions of Medium and, where identified, Residual Areas.

Combination Areas are disjoint unions of Small Areas to which the Catch Limit Algorithm is applied when Catch-cascading is used.

Management Area is a generic term denoting a Small, Medium, Large, Residual or Combination Area.

Catch Limit Algorithm is the process (described in Section 4) that is used to calculate a catch limit for a Management Area.

Years⁶ are consecutive periods of 12 months used for the compilation of time series of catches and abundance data for application of the Catch Limit Algorithm.

Catch-cascading⁷ is the process by which a catch limit calculated for a Combination Area is distributed among the Small Areas that make up the Combination Area in proportion to the calculated relative abundances in those Small Areas. When Catch-cascading occurs, the relative abundances for Small Areas within the Combination Area shall normally be calculated from the same estimates of absolute abundance as were used for the application of the Catch Limit Algorithm to the Combination Area. The calculated relative abundance in a Small Area shall be an appropriate form of weighted average of the available abundance indices for that Small Area, with the statistically appropriate weighting, except that each estimate shall also be further weighted by the factor 0.9,ⁿ where n is the number of years that have elapsed between the Year to which the estimate refers and the Year of the Catch Limit Calculation.

Catch-capping⁸ is the process by which Catch Limits calculated for Small Areas are adjusted by reference to those calculated for either Medium or Large Areas containing those Small Areas. It consists of the following rules. If the sum of the catch limits calculated for those Small Areas that make up a Medium (or Large) Area exceeds the catch limit calculated for the Medium (or Large) Area, then both the Small and Medium (or Large) Area catch limits shall apply in such a way that the maximum catch allowed in each Small Area is the appropriate Small Area catch limit and the maximum catch allowed in the Medium (or Large) Area is the Medium (or Large) Area catch limit. This definition does not preclude the possibility of applying Catch-capping to overlapping Medium Areas.

An Implementation involves the designation of the Management Areas and their boundaries and the selection of Catch-cascading and/or Catch-capping options for a particular species and Region. These designations and/or selections may be changed in a subsequent Implementation Review.

A Catch Limit Calculation is the process by which catch limits for a species in a Region are calculated for all Small (and where appropriate Medium or Large) Areas within that Region, as specified in Sections 3.3, 3.4 and 3.5, by application of the Catch Limit Algorithm as described in Section 4. This algorithm uses historic catch data and estimates of absolute abundance for each Management Area that meet the requirements of Section 3.2.

Implementations and Implementation Reviews are conducted by the Scientific Committee on a Regional basis. They involve the delineation of Small Areas and, where appropriate, Medium and Large Areas. A selection between possible options for the Catch-cascading and/or Catch-capping is made during an Implementation (Review), which includes the designation of Combination Areas as may be appropriate. This process is described as an Implementation on the first occasion it takes place for a species in a Region; subsequent revisions are termed Implementation Reviews.⁹ An Implementation (Review) shall take account of the available biological and operational data, including in particular those data pertaining to stock identity. An Implementation (Review) is conducted by species or other suitable taxonomic unit below the species level.¹⁰ Such taxonomic units should be treated separately for the purpose of Catch Limit Calculations (see Section 3) where the extent of geographical separation is sufficient to make this feasible. In the following text, 'species' should be taken to refer to taxonomic units below the species level where appropriate.

3.1 Scope and period of validity
Catch limits pertain to the first Year commencing after their calculation by the Scientific Committee, and for each of the following four Years.¹¹ A catch limit is calculated for each Small Area in a Region for each of these five Years. The five catch limits calculated for each Management Area shall be equal, except where adjustments are made under the phaseout rule specified in section 3.4. A Catch Limit Calculation involves the (re)calculation of catch limits for all Small Areas and, where appropriate, Medium or Large Areas in the Region. At the request of the Commission, the first of these catch limits calculated may alternatively refer to the Year in which the calculation takes place, and for each of the following four Years.

3.2 Data requirements¹²
3.2.1 Catch history
Time series of catches by sex shall be compiled for each of the Management Areas specified within the region, using the best available information. These catch histories shall cover a period beginning not later than the Year of the first recorded or estimated¹³ catch and ending with the Year preceding the first Year for which catch limits are to be calculated.¹⁴

If there are catches known to have occurred in the Region, but the Small Area in which they were taken is not known, they shall be assigned to the Small Area in which they are considered most likely to have been taken. Pro rata allocations are allowed. Where the sex ratio of catches is not accurately known, the best available estimate of the sex ratio shall be used to divide the catches; in the absence of any information, a 50:50 sex ratio shall be assumed. Unspecified catches of whales shall be allocated to species using the best available information on the species composition of the catch.¹⁵ Known or estimated numbers of whales struck and lost shall be added to the catches. If the timing of catches is uncertain, they shall be assigned to Years according to the best available information. No catches known to have occurred in the Region shall be omitted from the Catch Limit Calculation on grounds of uncertainty over their location, timing, sex ratio or other details. All known removals¹⁶ from a Region shall be included in the catch series.

3.2.2 Absolute abundance estimates
Absolute abundance data to be used in the calculation of catch limits shall have been obtained by direct methods,¹⁷ such as sightings surveys, and collected and analysed using methods approved by the Scientific Committee. Management Areas to which the Catch Limit Algorithm is applied should normally be surveyed at intervals not exceeding six years. The methods shall be such as to provide estimates of whale abundance that have acceptable levels of bias and precision. They shall also permit estimation of the variance of each estimate and of their variance-covariance matrix, or alternative variance-related statistics where appropriate.

Data for any sightings survey¹⁸ to be used to calculate abundance estimates for the purposes of conducting a Catch Limit Calculation shall be documented and provided to the Secretariat in computer readable data files before a specified time in advance of the Scientific Committee meeting during which the data are to be used. All such data should be archived by the Secretariat in an appropriate database such that abundance estimates can be calculated for any specified Small Area. Data should be in a fully disaggregated form so that estimates can be recalculated appropriately if the boundaries of Management Areas are altered. Once lodged with the Secretariat, these data shall be available to accredited scientists as defined in the Scientific Committee's Rules of Procedure.

Estimates of absolute abundance are required for each Management Area to which the Catch Limit Algorithm is to be applied under the procedures described in Section 3.3.¹⁹ For each such Management Area, a time series of absolute abundance estimates shall be calculated, along with an estimate of their variance-covariance matrix, or alternative variance-related statistics where appropriate. The approximate distributional properties of the abundance estimates shall also be determined. Care should be taken to avoid substantially underestimating the variance (or alternative variance-related statistic) of each abundance estimate used for input into the Catch Limit Algorithm.²⁰

The absolute abundance estimate for a given Year should ideally be calculated from data collected in that Year. Data collected in different Years may be used, for example to account for parts of the area that were not covered in that Year, to pool results from surveys conducted over consecutive or nearly consecutive Years in order to reduce variance, or to provide estimates of calibration factors, provided that appropriate statistical methods are used.²¹

Data from surveys conducted in different Years or at different times of year may only contribute to a single abundance estimate if adequate precautions are taken to avoid substantial double counting of whales due to migration or other factors. In the calculation of an absolute abundance estimate for a Management Area in a given Year, parts of the Area for which there are no absolute abundance estimates available at any time meeting the above specifications shall be treated as having an absolute abundance of zero.

The absolute abundance estimates should pertain to the total number of whales aged one year and above in the Management Area, regardless of any size limits that may be in force or the selectivity or otherwise of any past or present exploitation.²² Animals aged less than one year shall be excluded where possible.

3.3 Options for determination of catch limits
Catch limits shall always be set at the Small Area level and they shall be set for each Small Area in a Region. In addition, where Catch-capping is invoked at the Medium or Large Area level, corresponding catch limits will be set for those Medium or Large Areas. Catch limits for all Residual Areas within a Region shall be set at zero.

Catch limits for the total number of whales that may be taken in a season in each Small Area will be calculated by:

(a)

application of the catch limit algorithm to the Small Areas or, where appropriate, to Combination Areas, in which case Catch-cascading occurs; and

(b)

where appropriate, by adjustment of the Small Area catch limits calculated, with or without Catch-cascading, under (a) by either

(1)

application of the catch limit algorithm to one or more of the Medium Areas, followed by Catch-capping of the Small Area catch limits; or

(2)

application of the catch limit algorithm to one or more of the Large Areas, followed by Catch-capping of the Small Area catch limits.

Catch limits for the total number of whales that may be taken in a Year in Medium or Large Areas, as required when Catch-capping is invoked, will be calculated by application of the Catch Limit Algorithm to those Medium or Large Areas.

The decision for any particular species or Region on whether or not Catch-capping is to be applied, and if so whether it should be applied at the Medium or Large Area level, and whether or not Small Areas are to be combined for the purposes of Catch-cascading, will be made on the basis of biological evidence available to the Scientific Committee, and, where necessary, the results of computer simulation trials²³ conducted by the Scientific Committee. Where computer simulation trials are carried out, they shall, as far as possible, encompass the full range of plausible hypotheses (regarding, for example, stock identity) consistent with existing biological data.

3.4 Phaseout rule
The catch limits for a Small Area calculated under Section 3.3 shall be adjusted downwards when the time series of absolute abundance estimates used for the application of the Catch Limit Algorithm to the Small Area (or, if Catch-cascading has been applied, to the Combination Area containing it) does not include an absolute abundance estimate pertaining to a Year not more than eight years²⁴ prior to the Year to which the catch limit pertains. Under these circumstances, the catch limit for the Small Area shall be reduced by 20% of the unadjusted catch limit for that Small Area and Year for each year in excess of eight years that has or will have elapsed since the Year of the most recent such abundance estimate.²⁵ This rule shall also be invoked in a Small Area included in a Combination Area for Catch-cascading if the data used for the derivation of absolute abundance estimates for input to the Catch Limit Algorithm do not contain any survey effort in that Small Area within this eight year period.

3.5 Adjustments for recent sex ratios in the catch
If the proportion, P_f, of female whales in the total catch taken from a Small Area in the most recent five Years prior to the Catch Limit Calculation for which the catch data are available exceeds 50% , the catch limits for the Small Area calculated according to the procedure described in sections 3.3 and 3.4 shall be adjusted downwards by the ratio 0.5/P_f.²⁶ However, should the Scientific Committee decide it to be more appropriate, this adjustment ratio shall be determined from the proportion of females in the total catch taken from a union of Small Areas, and applied to the catch limit for each Small Area in the union. Further, the sex ratio adjustment shall be waived if the Scientific Committee agrees that the catches taken in the most recent five Years for which the catch data are available are too few to provide a useful indication of the expected future sex ratio of the catch.

The nominal catch limit for a Management Area shall be calculated using the algorithm defined below if at least one estimate of absolute abundance as defined in Section 3.2 is available for the Area in question. Otherwise, the nominal catch limit for the Management Area shall be zero.

4.1 Input data
The input data for application of the Catch Limit Algorithm for any Management Area shall include the time series of annual catches as detailed in Section 3.2.1 and the time series of absolute abundance estimates, along with their variance-covariance matrix or other appropriate variance-related statistics and a specification of the distributional form of the absolute abundance estimates, as specified in Section 2.2.2.

4.2 Population model
The following population dynamics model²⁷ shall be used:

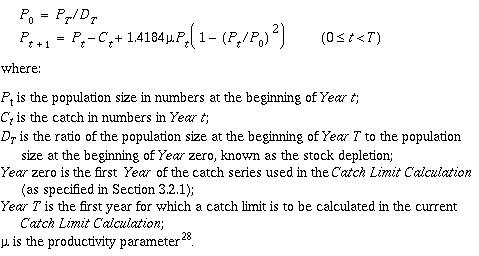
Provided there have been at least some catches, the population dynamics model is fully determined when the catch series and the values of D_T and 'mu' are specified. If there have been no catches, a nominal catch of one whale in Year zero is assumed.

4.3 Fitting of the model
The annual absolute abundance estimate (if there is one) for each Year t, is assumed to have expectation bP_t where b is the bias parameter. The joint likelihood function of the parameters b, D_T and 'mu' is determined using the absolute abundance estimates, the variance-covariance matrix of the absolute abundance estimates (or alternative variance-related statistics where appropriate) and information on their distributional form.

Unless there are specific indications to the contrary,²⁹ the absolute abundance estimates shall be assumed to be lognormally distributed with a variance-covariance matrix of the log estimates to be estimated from the data using methods judged appropriate by the Scientific Committee. In this case, the formula for the likelihood is:

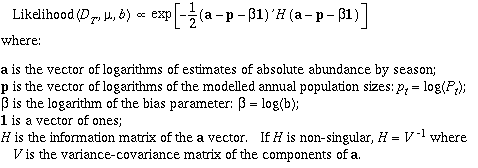
The stock depletion parameter D_T is assigned a prior probability distribution³⁰ that is uniform from zero to one, and zero outside this range.

The productivity parameter 'mu' is assigned a prior probability distribution³⁰ that is uniform from zero to 0.05, and zero outside this range.

The bias parameter b is assigned a prior probability distribution³⁰ that is uniform from zero to 5/3, and zero outside this range.

The above three prior distributions are treated as independent and combined accordingly to determine the joint prior distribution of the parameters D_T, 'mu' and b.

The joint 'posterior' distribution of the parameters D_T, 'mu' and b is defined as follows:

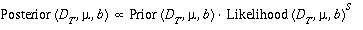
where s, the scale parameter, is set equal to 1/16. The presence of the scale parameter represents an intended deviation from a strictly Bayesian approach.

4.4 The catch control law
The internal catch limit, L_T, is the following function of D_T, 'mu' and P_T:

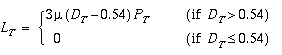
The marginal posterior distribution of L_T is obtained by integration of the joint posterior distribution of (D_T, 'mu', b). This requires that, for each value of L_T, the joint posterior distribution of (D_T, 'mu', b) is to be integrated over the subset of parameter space that corresponds to that value of L_T. The nominal catch limit is equal to the lower 41.02 percentile of the marginal posterior distribution of L_T.³¹

4.5 Computation
All steps in the above algorithm for the calculation of the nominal catch limit shall be performed using a computer program validated by the IWC Secretariat and with sufficient numerical accuracy that the calculated nominal catch limit is numerically accurate to within one whale.

(1)

The trials carried out to date have largely been based on simulated management of baleen whales with breeding grounds in lower latitudes and feeding grounds in higher latitudes, and with whaling operations and abundance surveys restricted to higher latitudes. Thus, while the species may be distributed over an entire Region as defined here, most data will pertain only to a restricted part of the Region. While it is believed that the framework for calculation of catch limits specified here will be sufficiently flexible for management of species in Regions not directly matching the conditions simulated so far, this needs to be affirmed by the additional simulation trials required before implementation of the RMP in such cases. This would be especially important in the case of humpback or right whales, for which there is a possibility of whaling in the breeding grounds, on feeding grounds and on migrations between these in the one year.

The development of the RMP has been a long and difficult task, involving a wide range of scientific and technical issues and a thorough and extensive testing process. The Scientific Committee has recommended a protocol for evaluating amendments to the RMP which is given in Rep. int. Whal. Commn 44:47-8 (Item 7.1.4).

1. Definitions

(2)

The judgement on whether or not differences in proportions may be substantial will, in the first place, be based on estimates of movements and rates of mixing, and on relevant operational factors. Where the size of a proposed Small Area is such that potential differences in the proportions might be substantial, its acceptability will be judged on the basis of the risk of inadvertent depletion of some of the stocks in the Region, as estimated from suitable simulation trials. Conducting such simulation trials will be a normal part of the initial implementation of the RMP to a Region and species. Additional trials may also be necessary where it is proposed to increase the size of existing Small Areas.

(3)

Medium Areas play a secondary role in the RMP, in that they are used only when Catch-capping is applied; it is not necessary for application of the RMP for any Medium Areas to be defined. In cases where Medium Areas can be identified with some confidence, so that Medium Areas approximate to ranges of actual stocks, Catch-capping is most appropriately carried out at the Medium Area level, rather than at a Large Area level. See also annotation 8.

(4)

As indicated, normally Large Areas will coincide with Regions. An example of when a Large Area may be smaller than a Region is the case in which there is a geographically isolated stock of whales within the Region which does not mix with other whale stocks within the Region.

(5)

Normally, in cases where the whales migrate to higher latitudes, these Residual Areas will be confined to lower latitude areas within a region. In such cases, they will normally also be unsurveyed, and so will be assigned an absolute abundance of zero. As indicated in Section 3.3, catch limits are set at zero for Residual Areas.

(6)

A Year is normally a calendar year for Northern Hemisphere Regions and split-years (for example, July 1 - June 30) for Southern Hemisphere Regions. Where possible, a Year should be compatible with the whaling season established in terms of the definition in the Schedule.

(7)

Where Small Areas identified in a region are also quite small in size, it is likely that the absolute abundance estimates for these Small Areas will have large variances associated with them. On the other hand, estimates of absolute abundance for some combinations of these Small Areas may have considerably greater precision. Provided sufficient evidence exists to warrant combining some Small Areas, the process of Catch-cascading can be used to take advantage of this greater precision. In calculating the relative abundances in the Small Areas making up a Combination Area, a weighted average of past abundance indices for those Small Areas is used. The additional factor of 0.9ⁿ is included to downweight abundance data from Years separated far in time from the Year of the Catch Limit Calculation. Criteria for deciding whether or not Catch-cascading should be applied are given in Section 3.3.

An example of the calculation involved is as follows. If the absolute abundance estimates are treated as being lognormally distributed, then the relative abundance for a Small Area would normally be calculated using the following formula.

Let:

a = vector of log abundance estimates in the Small Area;
t_i = difference between the current Year and the Year of the ith estimate;
F = information matrix of a.

If F is non-singular, F = V^-1 where V is the variance-covariance matrix of a. G is the matrix such that G_ij = F_ij(0.9) ^-(t_i+t_j)/2

The relative abundance in the Small Area is given by:

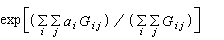
(8)

Catch-capping is a process designed to ensure that catch limits calculated individually for some Small Areas are not inappropriately large, as is possible in some cases of uncertain stock identity. As indicated in Section 3.3, whether or not Catch-capping is invoked in the Catch Limit Calculation for a species in a particular Region will depend on examination of available data and possibly simulation trials for that species and Region. Catch-capping, if it is invoked, will be carried out at the Medium or Large Area level depending on the degree of certainty existing about the identification of Medium Areas. Where that degree of certainty is relatively high, Catch-capping should be carried out at the Medium Area level. Where no Medium Areas are identified for a species and region, Catch-capping should be carried out at the Large Area level, if invoked. Where Medium Areas are identified, but only tentatively, the decision as to whether any Catch-capping should be carried out at the Medium or Large Area level should be determined from results of appropriate simulation trials.

Catch-capping Can be applied together with Catch-cascading. In this case, after the Small Area catch limits have been calculated under Catch-cascading, the capping option is invoked.

2. Implementations and Implementation Reviews

(9)

An Implementation is required before the Catch Limit Algorithm can be applied to a new species and Region for the first time. An Implementation Review for a species and Region should normally be scheduled for not more than five years since the completion of the previous Implemenlalion (Review). In some cases an Implementation (Review) may require the specification and running of further implementation trials, especially when major changes to Management Area boundaries or the selection of different options for Catch-capping and/or Catch-cascading than those currently used is contemplated. In such cases the Implementation Review would probably not be completed at a single meeting. In the meantime, Catch Limit Calculations continue to be based on the existing Management Areas and options.

In some cases, it may be appropriate to carry out an Implementation Review less than 5 years after the previous Implementation (Review). This would be warranted, for example, if important new evidence on stock identity becomes available, if major advances are made in methodology of calculating absolute abundance estimates, if major changes occur in the areas covered by the abundance surveys, or if other evidence becomes available to the Scientific Committee suggesting that the premises on which the previous Implementation (Review) was conducted are no longer appropriate.

(10)

Normally, Implementation (Reviews) will be carried out at the species level. However, if sub-species, varieties or different morphological forms of baleen whales exist in a Region such that they can be identified in catches and separate absolute abundance estimates can be obtained for them, then Implementation (Reviews) should be conducted separately, provided the degree of geographical separation is sufficient to allow this.

3. Catch Limit Calculations
3.1 Scope and period of validity

(11)

To provide an uninterrupted series of catch limits, a new Catch Limit Calculation will normally be required not more than five years after the preceding one. However, a Catch Limit Calculation should be carried out sooner than this if a new abundance estimate meeting the requirements of Section 3.2.2 becomes available. Even if no new abundance estimate has become available, it could be necessary to carry out the new Catch Limit Calculation up to one year before the expiry of the current five-Year series of catch limits, to ensure timely availability of the resulting figures. In the event of difficulties of finalising the analysis of new abundance data in time to be used in the Catch Limit Calculation for the next five-Year period, the Catch Limit Calculation shall nevertheless be carried out with the existing agreed data.

3.2 Data requirements
3.2.1 Catch history

(12)

In addition to the requirements outlined in Section 3.2, data and methods for analysing them that are used in the application of the RMP should meet the minimum standards described in Rep. int. Whal. Commn 44:44 (Item 7.1.2).

(13)

For stocks for which exploitation started relatively recently, the catch history over the entire period of exploitation will be well known. For other stocks, however, where exploitation has extended over many years and possibly intermittently over centuries, records for early catches may be incomplete, or gaps may exist. The intent here is that the catch histories for use with the RMP should extend as far back as possible. Where there are no gaps in a long historical record of catches, the catch series used in Catch Limit Calculations shall start in the first season for which the catch has been recorded or estimated sufficiently reliably. Where there are gaps, or there is major uncertainty about the early catch history, selection of the first Year will be made on a case by case basis.

The RMP has been demonstrated to be robust to considerable uncertainties in catch histories in single stock robustness trials (Rep. int. Whal. Commn 42:272).

(14)

In the event of catch data for the most recent years not yet being available, input to the Catch Limit Algorithm shall assume that the catches taken are equal to the limits set for those Years.

(15)

Where the information is insufficient to allocate catches to species sufficiently reliably, the potential consequences of incorrect allocations may need to be examined by simulation trials.

(16)

The population model used in the Catch Limit Algorithm (see Section 4) effectively assumes that all whales that die from causes other than those resulting from natural mortality are included in the catch history. Thus, known 'indirect' catches, e.g. whales killed through entanglement in fishing gear, should also be included in the catch history, in addition to whales caught or struck and lost in direct whaling operations. On the other hand, stranding is assumed to be part of the process of natural mortality, and numbers of whales stranded should not be included in the catch history.

3.2.2 Absolute abundance estimates

(17)

In the early stages of development of the RMP, it was envisaged that absolute abundance estimates, relative abundance indices, or both could be used. The difficulty with use of relative abundance indices that are collected as part of or associated with catching operations of the type carried out prior to the development of the RMP, is that the precise relationship between the index and the true absolute abundance is rarely known. These issues were discussed at the CPUE workshop, at which the types of information necessary to clarify this relationship were also identified (Rep. int. Whal. Commn 38:157-62). As this relationship has remained unresolved, the possible use of such data was dropped for the present. Possible use of relative abundance indices other than those associated with catching operations was not investigated during development of the RMP.

Note that the above does not preclude the use of estimates of relative abundance during Catch-cascading (see annotation 7) or in analysing abundance data collected in different Years (see Section 3.2 and annotation 2l).

In some circumstances, the best available estimates of absolute abundance may come from mark-recapture analyses, e.g. those resulting from photo-identification studies. The properties of such estimates, and the implications of these with respect to possible uncertain stock identity and migration patterns need to be evaluated before estimates of abundance based on them may be used when implementing the RMP for a particular species and Region. Until this is done, sightings surveys or other direct methods of estimation with similar statistical properties remain the primary tools for obtaining suitable estimates of absolute abundance for Catch Limit Calculations.

(18)

The types of data that are required fall into two categories: data necessary for standard analyses (e.g. sightings effort data and sightings records) and ancillary data (as appropriate according to the analyses to be carried out, e.g. dive-time records) (Rep. int. Whal. Commn 44:44-5).

(19)

In the simulation trials of the RMP carried out so far, it has been assumed that absolute abundance estimates are available for effectively all the Management Areas within the Region being assessed. As indicated later in Section 3.2, Management Areas for which no suitable estimates of absolute abundance are available are treated as having an absolute abundance of zero. This, along with the possible application of Catch-capping described in Section 2.3, makes adequate provision for cases where surveys have not been conducted for some parts of the range in the Region being assessed, provided the unsurveyed area does not form too large a proportion of that range.

(20)

This is because trials have shown adverse behaviour when there is a high probability of substantial underestimation of the variance. This can occur even when the variance estimator is statistically unbiassed, but has a high variance. Estimators for the variance (or alternative variance related statistics) should take into account, to the extent possible, all sources of observation error, and should not themselves have such high variance that there is a serious risk of markedly overestimating the precision of an abundance estimate. These remarks do not apply to zero abundance estimates, which should be handled in the way described in annotation 29 unless a more appropriate alternative method is available. Simulation trials have shown that process error may need to be taken into account when the observation error is low and the process error is high. Some examples in this regard may be found in Rep. int. Whal. Commn 44:75-6.

Note:
Observation error is the sampling error arising from the survey methods and design. The level of observation error is inversely related to the amount of survey effort, provided that the survey is well designed.

Process error reflects the extent to which abundance estimates from repeat surveys of the same area in successive years will vary more than would be expected on the basis of the observation error alone, for example due to variations in the numbers of whales moving into or out of the survey area.

(2l)

Statistical methods to be used in the calculation of absolute abundance estimates from data collected in different years shall ensure, inter alia, that (i) no piece of data receives undue weight; (ii) the absolute abundance estimate is referred to the most appropriate Year; (iii) the data contributing to an absolute abundance estimate for any Management Area in a given Year shall normally all have been collected within a ten year period, and where possible not more than five years earlier or later than the Year to which the abundance estimate refers; and (iv) in the case of a Small Area or a Combination Area, except for contributions to calibration factors, data collected in a Year other than that to which the estimate refers shall not contribute disproportionately to the abundance estimate. A contribution to the abundance estimate of more than 50% would normally be considered disproportionate. For some stocks of whales currently at low levels of abundance, it may be necessary to pool data over a period longer than ten years in order to obtain reliable estimates of some calibration factors. It is possible that in the future, appropriate alternative statistical methods may be developed for calculating time series of absolute abundance estimates in which data from all Years are analysed together, e.g. methods based on generalised linear models (SC/F92/Mg8; Rep. int. Whal. Commn 44:93-4). For such methods, the above requirements may need revision.

(22)

In the simulation trials conducted so far, it has been assumed that estimates of absolute abundance correspond to whales of all ages from one year upwards.

3.3 Options for determination of catch limits

(23)

The Committee has recommended that suitable case-specific simulation trials be carried out prior to the initial implementation of the RMP for each species and Region. These have been termed 'implementation simulation trials', to distinguish them from the more generic robustness trials used during the development of the RMP.

Where simulation trials are used during implementation to evaluate the appropriateness or otherwise of Catch-cascading and/or Catch-capping, and in the latter case whether at Medium or Large Area level, judgements will be based on comparisons of performance of the different options against a base case where catch limits are calculated and set by Small Area only. The addition of Catch-capping to other options leads to the setting of catch limits lower than or equal to those which would be set in the absence of Catch-capping. Where the performance of suitable simulation trials of the base case option for setting catch limits is satisfactory in terms of statistics related to lowest and final depletion levels, it would not normally be judged necessary to invoke Catch-capping ('depletion' is defined in Section 4.2). However, where the performance of the base case option is judged unsatisfactory in terms of the depletion statistics, and this is rectified when one of the Catch-capping options is used, Catch-capping at the relevant level shall be invoked.

Catch-cascading normally leads to higher catch limits than the base case option. Accordingly, Catch-cascading may only be invoked when simulation trials show that it does not lead to unsatisfactory performance on depletion statistics related to lowest and final depletions.

Examples of examination of these issues in the context of potential implementation of the RMP to Southern Hemisphere and North Atlantic minke whales are given in Annexes E and F of the 1992 Report of the Scientific Committee (Rep. int. Whal. Commn 43:104-14 and 115-29).

3.4 Phaseout rule

(24)

Discussion of issues relating to the selection of this time period is recorded in Rep. int. Whal. Commn 44:48 (Item 9).

(25)

This provision will ensure that the catch limit will be reduced linearly to zero in five years. All five catch limits, including phaseout adjustments, are to be calculated at the time of the Catch Limit Calculation. This allows prior warning to the Commission and member governments that future phaseouts will occur within five years unless new abundance estimates meeting the requirements of Section 3.2 become available and a Catch Limit Calculation is performed.

3.5 Adjustments for recent sex ratios in the catch

(26)

An example may help clarify this formulation. Suppose that in the 5 years prior to the Catch Limit Calculation, during which the annual catch limit was 100 whales, the total catch from the Small Area comprised 200 males and 300 females, i.e. P_f = 300/(200 + 300) = 0.6. Suppose also that prior to the sex ratio adjustment, the annual catch limit indicated by the Catch Limit Algorithm for each of the next five years is 132 whales. The adjusted catch limit is then:

132 x 0.5/P_f = 132 x 0.5/0.6 = 110 whales per annum

Note that the aim of the Catch Limit Algorithm in setting the pre-adjustment catch limit is that this comprise equal numbers (66 in this case) of males and females. The intent of the adjustment is that no more than 66 females will be caught: if the female proportion remains at 0.6, this will be achieved exactly by the adjustment process because 0.6 x 110 = 66.

4. Catch limit algorithm
4.2 Population model

(27)

The population dynamics model used here has the form of a discrete time version of the Pella-Tomlinson model. Neither the form of model used, nor its parameter values, are meant to give an accurate representation of the population dynamics of baleen whales. Rather, it is a model which, when used as an integral part of the Catch Limit Algorithm, has been demonstrated to allow robust calculation of catch limits.

(28)

The parameter 'mu' is related to the MSY rate. For the population model used,

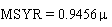
4.3 Fitting of the model

(29)

An example where the lognormal assumption cannot be used is when the estimate of absolute abundance is zero. Zero estimates of absolute abundance arise when no sightings of the target species are made on primary effort during a survey of an area. This should not be a frequent occurrence, but such estimates should not be ignored when they do occur.

Although several factors contribute to the variance of an estimate of absolute abundance, the variance is dominated by the variance in the number seen when the number of sightings is very low. The variance of the number of sightings will be at least as high as the variance of a random variable with a Poisson distribution with expectation equal to the expectation of the number of sightings. The number of sightings refers to the number of schools or groups, rather than to individual animals.

The expected number of sightings, E(n), is proportional to the true absolute abundance, P:

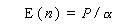
The parameter 'alpha' represents the estimate of absolute abundance that would have been obtained had there been exactly one sighting. This will be a function of the survey effort, the size of the area, and survey parameters that may need to be estimated by adopting values from similar surveys. Ignoring the variance of 'alpha', the likelihood of the zero estimate of absolute abundance is the following function of the true absolute abundance:

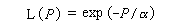
Since the only covariance between the absolute abundance estimate and other absolute abundance estimates is that due to the 'alpha' parameter, whose variance is being ignored, the joint likelihood function of the zero estimate of absolute abundance and the remaining estimates is taken to be the product of the respective likelihood functions.

The information about the zero estimate of absolute abundance that needs to be supplied to the Catch Limit Algorithm is: (i) the Year of the zero estimate; (ii) the fact that it is a zero estimate; and (iii) the value of the 'alpha' parameter. The computer program implementing the Catch Limit Algorithm that has been validated by the Secretariat has the facility to handle zero estimates of absolute abundance in this manner. P is identified with the simulated population size generated by the Catch Limit Algorithm's internal calculations.

Since the treatment above ignores some contributions to the variance of a zero estimate of absolute abundance, it assigns more weight to a zero estimate than is strictly warranted.

(30)

Despite their appearance, the prior distributions assumed here are not standard Bayesian priors on the selected parameters reflecting prior beliefs about the likely distribution of the corresponding biological parameters. The procedure adopted here is Bayes-like, rather than strictly Bayes. The distributions and ranges were selected to provide 'optimum' performance in relation to a set of agreed performance statistics in simulation trials. If likely ranges and distributions of the corresponding biological parameters change from current perceptions, the appropriate way to take account of these changed perceptions is to revise the simulation trials, and if appropriate change the tuning (Rep. int. Whal. Commn 42:55) of the procedure, rather than altering the 'priors'.

4.4 The catch control law

(3l)

This percentile was arrived at by a process detailed in Rep. int. Whal. Commn 44:153-167 to implement the Commission's choice (Rep. int. Whal. Commn 42: 47-48) of a 0.72 tuning level.

_